Billet en cours de rédaction
Principia Mathematica
Philosophiæ Naturalis Principia MathematicaQ de Isaac Newton (1687) est une oeuvre majeure dans l’histoire des sciences. Tout ce que j’en sais avant de débuter ce projet c’est que les lois mathématiques qui y figurent servent à décrire le monde physique, principalement le mouvement des astres et la gravitation. De plus, je me souviens que Newton y développe sa propre méthode de calcul infinitésimal (dérivé+intégral) en concurrence avec Liebniz sur qui est le premier.
Pratiques de citation
Principia est un objet littéraire et scientifique idéal pour étudier les pratiques de citation que l’on y trouve car 1) on peut observer comment Newton cite ceux qui l’on précédé et tenter d’expliquer pourquoi; et 2) cette oeuvre a été lue et étudiée par un très grand nombre de scientifiques dans les siècles qui ont suivi (impact).
Méthode 1 : annotation manuelle
J’ai parcouru visuellement tout le livre pour repérer des indications d’attribution, de citations, de mentions, etc.
J’ai trouvé principalement :
Beaucoup de mentions de personnes (entités nommées d’individus) et un peu d’institutions ou de groupes. Ils ont été indexé au fil de l’eau dans Wikidata avec la propriété acknowledged (P7137) et avec le qualifiant object named as (P1932) pour décrire la ou les formes que le nom prend dans le texte.
Un peu de mentions de travaux. Ils ont été indexé au fil de l’eau dans Wikidata avec la propriété cites work (P2860) et avec le qualifiant object named as (P1932) pour décrire comment l’oeuvre est décrite dans le texte.
Inconvénients
Si on veut calculer qui est cité et combien de fois et où, il faut extraire toutes ces mentions et créer un script qui les compte. Et encore, certains termes trop génériques risquent de générer des faux-positifs (exemple : Conics). Idéalement, il aurait fallu créer un fichier XML-TEI et le baliser.
Avantages
Cela permet de parcourir tout le document et de découvrir progressivement des tendances et se faire une culture sur les éléments mentionnés. Parfois, le repérage d’un astronome a été un vrai défi pour repérer qui pouvait être tel ou tel personnage cité.
Par 9 fois, il m’a fallu créer de nouveaux éléments Wikidata pour des entités (personnes ou travaux) qui n’existaient pas encore dans Wikidata :
- Legum Allegoriæ (Q138348789)
- Valentinus Estancius (Q138341375)
- Ponthæus (Q138341287)
- Samuel Colepress (Q138334903)
- Varin (Q138334135)
- Institutionum astronomicarum (Q138332932)
- Conics (Q138296602)
- The two Books of Apollonius Pergaeus… (Q138296556)
- Ephemerides novae motuum coelestium (Q138354676)
On découvre et on mémorise naturellement des tendances. Par exemple :
- Les personnes sont souvent citées en série ;
- Les personnes sont soient des observateurs, soient des théoriciens (math, physique, etc.) ;
- Les personnes sont souvent citées au début ou à la fin pour leurs théories ;
- Les italiques sont parfois utilisées pour les personnes et les oeuvres ;
- Les noms des personnes sont très succincts, voire ne correspondent pas à la forme « canonique » de leur nom tels que nous les connaissons aujourd’hui : espaces dans le nom, double L ou simple L, nom latin ou nom vulgaire, parfois nommé d’une manièr et parfois d’une autre, etc. ;
- Galilée, dont les Principia prolongent les travaux, n’est pas beaucoup cité ;
- Il y a une section de citations bibliques ;
Méthode 2 : traitement automatisé par IAg
AstaLab AutoDiscovery
J’ai testé AstaLab AutoDiscovery (AA) qui est censé être un «générateur d’hypothèses». J’ai téléchargé le texte complet des Principia depuis WikiSource au format Plain Text. Je l’ai soumis à AA en demandant 10 hypothèses. Ce n’était pas fameux mais la seule hypothèse intéressante était celle concernant les entités nommées citées. Voici ce qu’il dit :
The citations of historical scientific authorities (e.g., Kepler, Galileo, Euclid, Descartes) are not uniformly distributed but appear in distinct bursts, suggesting that Newton engages with specific intellectual lineages in concentrated thematic blocks rather than continuously. (source)
De manière plus intéressante encore, AA fournit le code Python pour produire cette déclaration. Le voici :
import numpy as np
import matplotlib.pyplot as plt
import re
import os
from scipy.stats import kstest
from collections import Counter
# Define the target names of historical scientists
# Using a predefined list as suggested to avoid NER model dependency issues
target_names = [
"Kepler", "Galileo", "Euclid", "Descartes", "Copernicus",
"Tycho", "Brahe", "Huygens", "Hooke", "Halley", "Boyle",
"Archimedes", "Apollonius", "Wren", "Wallis", "Leibniz", "Newton"
]
# File path setup
filename = "The_Mathematical_Principles_of_Natural_Philosophy_(1846).txt"
filepath = os.path.join("..", filename)
# Check if file exists in parent dir, otherwise check current dir
if not os.path.exists(filepath):
filepath = filename
if not os.path.exists(filepath):
print(f"Error: File {filename} not found in .. or current directory.")
exit(1)
print(f"Loading dataset from: {filepath}")
with open(filepath, 'r', encoding='utf-8', errors='ignore') as f:
text = f.read()
# 1. Identify locations of names
print("Identifying name occurrences...")
# Use regex with word boundaries for robustness
pattern = r'\b(' + '|'.join(target_names) + r')\b'
matches = list(re.finditer(pattern, text, re.IGNORECASE))
occurrences = []
found_names = []
for match in matches:
occurrences.append(match.start())
# Normalize name to Title Case for counting
found_names.append(match.group(1).title())
if not occurrences:
print("No target names found in the text.")
exit()
# Convert to numpy array
positions = np.array(occurrences)
total_length = len(text)
# 2. Time-series-like array (positions are the events)
# Normalize positions to [0, 1] for KS test against uniform distribution
normalized_positions = positions / total_length
# 3. Kolmogorov-Smirnov Test
# Test if the observed normalized positions follow a uniform distribution [0, 1]
stat, p_value = kstest(normalized_positions, 'uniform')
# 4. Dispersion Index of distances
# Calculate distances (inter-arrival times) between consecutive names
intervals = np.diff(positions)
if len(intervals) > 0:
mean_interval = np.mean(intervals)
var_interval = np.var(intervals, ddof=1)
# The user requested variance/mean of the distances
dispersion_metric = var_interval / mean_interval
# Also calculating Coefficient of Variation (CV) which is dimensionless
cv = np.std(intervals, ddof=1) / mean_interval
else:
mean_interval = 0
var_interval = 0
dispersion_metric = 0
cv = 0
# Generate Summary
counts = Counter(found_names)
print("\n##### Analysis Results #####")
print(f"Total Citations Found: {len(positions)}")
print(f"Unique Scientists Cited: {len(counts)}")
print("\nTop 10 Most Cited Scientists:")
for name, count in counts.most_common(10):
print(f" {name}: {count}")
print("\n##### Statistical Test Results #####")
print(f"KS Test Statistic: {stat:.4f}")
print(f"KS Test p-value: {p_value:.4e}")
if p_value < 0.05:
print("Result: The distribution of names is significantly different from Uniform (p < 0.05).")
else:
print("Result: The distribution is consistent with Uniform.")
print(f"\nMean Distance between citations: {mean_interval:.2f} characters")
print(f"Variance of Distances: {var_interval:.2f}")
print(f"Dispersion Metric (Var/Mean of distances): {dispersion_metric:.2f}")
print(f"Coefficient of Variation (Std/Mean): {cv:.2f}")
if cv > 1:
print("Interpretation: CV > 1 suggests clustering/burstiness.")
elif cv < 1:
print("Interpretation: CV < 1 suggests regularity.")
else:
print("Interpretation: CV ~ 1 suggests random Poisson process.")
# Visualizations
plt.figure(figsize=(15, 6))
# Subplot 1: Rug Plot
plt.subplot(1, 2, 1)
plt.eventplot(positions, orientation='horizontal', colors='black', linewidths=0.5)
plt.title("Rug Plot of Scientific Authority Citations")
plt.xlabel("Position in Text (Characters)")
plt.yticks([])
plt.xlim(0, total_length)
# Subplot 2: Histogram
plt.subplot(1, 2, 2)
plt.hist(positions, bins=50, color='skyblue', edgecolor='black', alpha=0.7)
plt.title("Histogram of Citation Density")
plt.xlabel("Position in Text (Characters)")
plt.ylabel("Frequency")
plt.tight_layout()
plt.show()Comme on peut le voir, il suffit de changer le contenu de la variable target_names avec tous les noms que l’on veut pour regénérer un nouveau résultat testant la présence d’entités nommées tout le long du texte.
Extraire les noms de Wikidata
On va extraire tous les qualifiants de acknowledges avec :
SELECT ?value ?valueLabel ?qualifierValue
WHERE {
wd:Q205921 p:P7137 ?statement .
?statement ps:P7137 ?value .
OPTIONAL {
?statement pq:P1932 ?qualifierValue .
}
SERVICE wikibase:label {
bd:serviceParam wikibase:language "fr,en".
}
}Ensuite, on exporte le résultat au format tsv ou csv, on supprime les deux premières colonnes pour ne garder que la colonne qualifierValue. On fait un peu de ménage dedans :
- sans
Mr.ouDr.ouM. - sans initiales, ni extensions du nom (
Pappus of AlexandriadevientPappus) - supprimer les troncatures emboîtées pour éviter les doubles comptages (ex: pour
Samuel ColepressetColepress: ne garder queColepress)
Cela donne names.csv
Code modifié
Remplacer la variable target_names plus haut par :
target_names = [
"Horrox", "Egyptians", "Romans", "Anaximander", "Pythagoreans", "Numa Pompilius", "Democritus", "Eudoxus", "Calippus", "Crabtrie", "Marius", "Townley", "Romer", "Ricciolus", "Kircher", "Pappus", "Halley", "Royal Society", "Galileo", "Wren", "Wallis", "Huygens", "Huygenian", "Hugenius", "Mariotte", "Euclid", "Hook", "Hooke", "Apollonius", "Archimedes", "Snellius", "Des Cartes", "Grimaldus", "Collins", "Slusius", "Huddens", "Desaguliers", "Sauveur", "Copernicus", "Copernican", "Borelli", "Townly", "Cassini", "Pound", "Kepler", "Keplerian", "Bullialdus", "Ptolemy", "Vendelin", "Street", "Tycho", "Mercator", "Norwood", "Picart", "Richer", "Varin", "des Hayes", "Couplet", "Feuillé", "de la Hire", "Colepress", "Sturmy", "Machin", "Pemberton", "Flamsted", "Hevelius", "Cysatus", "Bayer", "Kirch", "Julius Cæsar", "Ponthæus", "Cellius", "Galletius", "Ango", "Storer", "Montenari", "Zimmerman", "Estancius", "Simeon", "Matthew Paris", "Aristotle", "Auzout", "Petit", "Gottignies", "Bradley", "Hipparchus", "Cornelius Gemma", "God", "Pocock", "John", "Moses", "Aaron", "Pythagoras", "Cicer.", "Thales", "Anaxagoros", "Virgil", "Philo Allegor.", "Aratus", "St. Paul", "David", "Solomon", "Job", "Jeremiah", "Pharaoh", "Philolaus", "Aristarchus", "Plato"
]Le code et le corpus se trouvent à l’adresse XXX.
Contrôle (manuel)
Avec Notepad++, utiliser quelques noms pour les compter manuellement (Fonction Rechercher + Compter) et vérifier que le code fonctionne.
Résultats
##### Analysis Results #####
Total Citations Found: 574
Unique Scientists Cited: 105
Top 10 Most Cited Scientists:
God: 65
Halley: 32
Kepler: 29
Royal Society: 26
Flamsted: 24
Hevelius: 21
Huygens: 20
Hook: 19
Hooke: 16
Montenari: 15
##### Statistical Test Results #####
KS Test Statistic: 0.3040
KS Test p-value: 1.4816e-47
Result: The distribution of names is significantly different from Uniform (p < 0.05).
Mean Distance between citations: 2502.37 characters
Variance of Distances: 74249546.11
Dispersion Metric (Var/Mean of distances): 29671.65
Coefficient of Variation (Std/Mean): 3.44
Interpretation: CV > 1 suggests clustering/burstiness.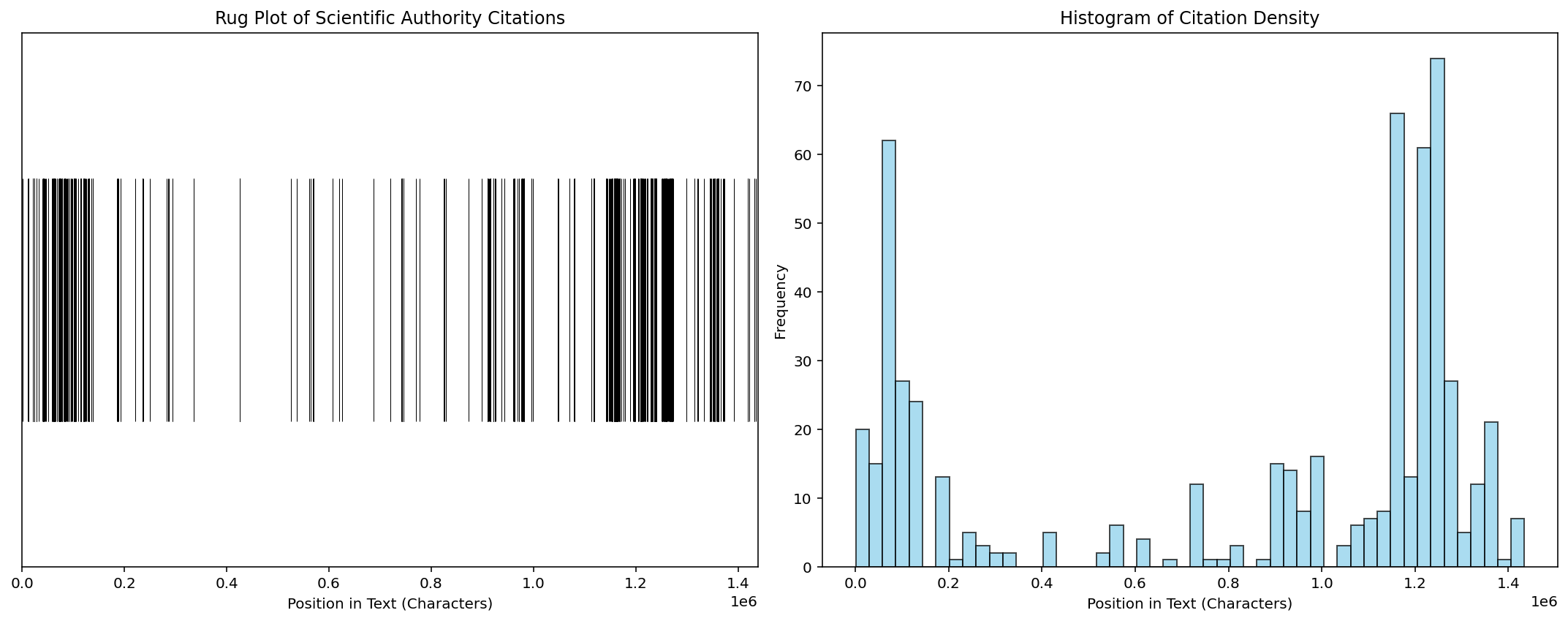
Plus de contexte!
Cette analyse en aveugle des Principia a besoin d’être contextualisé par la lecture de la conversation scientifique historique sur le sujet (l’historiographie). On pourra bientôt lire le livre (fin 2026) The Winding Trail to Newton’s Principia Mathematica de Jed Z. Buchwald et Mordechai Feingold. En attendant, on pourrait lire d’autres travaux sur le même sujet par ses deux auteurs.